Structs and interfaces for area calculations. More...

Go to the source code of this file.
Macros | |
| #define | YAC_AREA_TOL ((0.02 * 0.02) / (6371.2290 * 6371.2290)) |
Functions | |
| double | yac_triangle_area (struct yac_grid_cell cell) |
| Calculate the area of a triangle on a unit sphere. | |
| double | yac_cell_area (struct yac_grid_cell cell) |
| Calculate the area of a cell on a unit sphere. | |
| double | yac_pole_area (struct yac_grid_cell cell) |
| Calculate the area of a cell in a 3d plane on a unit sphere. | |
| double | yac_planar_3dcell_area (struct yac_grid_cell cell) |
| Area calculation on a unit sphere of a planar polygon in 3D. | |
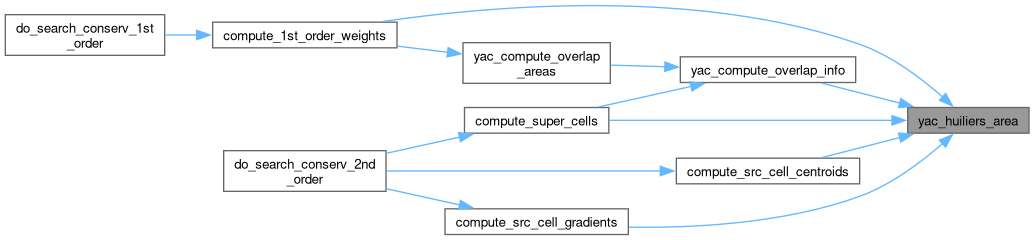
| double | yac_huiliers_area (struct yac_grid_cell cell) |
| Area calculation on a unit sphere taken from ESMF based on L'Huilier's Theorem. | |
| double | yac_huiliers_area_info (struct yac_grid_cell cell, double *barycenter, double sign) |
Detailed Description
Structs and interfaces for area calculations.
Definition in file area.h.
Macro Definition Documentation
◆ YAC_AREA_TOL
| #define YAC_AREA_TOL ((0.02 * 0.02) / (6371.2290 * 6371.2290)) |
an area of 20m x 20m on the Earth Surface is equivalent to an area on the unit sphere:
- Examples
- test_area.c.
Function Documentation
◆ yac_cell_area()
| double yac_cell_area | ( | struct yac_grid_cell | cell | ) |
Calculate the area of a cell on a unit sphere.
Generalized version of triangle_area
The algorithm is based on Girards' theorem and formula.
Converted to c by Rene Redler, MPI-M.
Vertex coordinates need to be provided as cartesian coordinates
The algorithm is based on Girards' theorem and formula.
R: Earth radius n: number of vertices pi: guess what Theta: Sum of inner angle of the element (in rad)
The Formula reads as
S = [ Theta - (n-2) * pi ] * R*R
- Parameters
-
[in] cell cell for which he area shall be calculated
- Returns
- area of the triangle
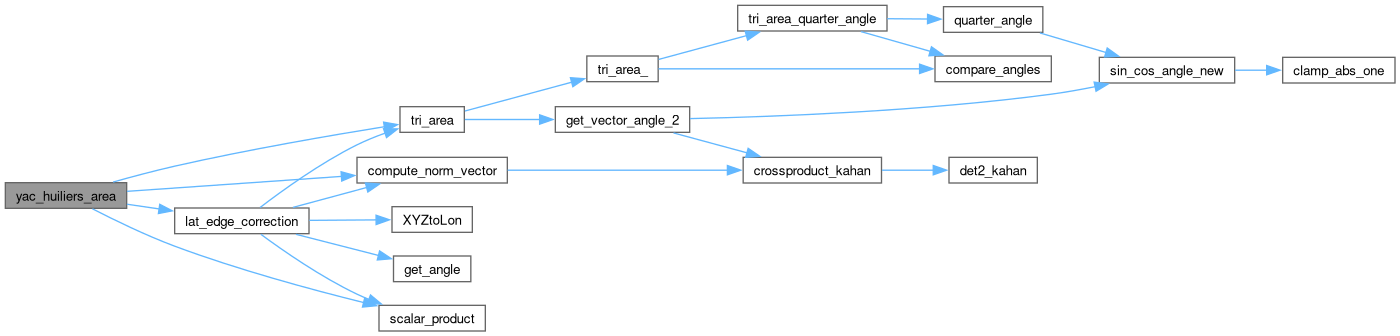
◆ yac_huiliers_area()
| double yac_huiliers_area | ( | struct yac_grid_cell | cell | ) |
Area calculation on a unit sphere taken from ESMF based on L'Huilier's Theorem.
(http://mathworld.wolfram.com/LHuiliersTheorem.html)
(http://mathforum.org/library/drmath/view/65316.html)
(http://math.stackexchange.com/questions/9819/area-of-a-spherical-triangle)
The cell in split up into triangles that all have one corner in common, then the area for each of the triangle is computed and summed up to build the area of the cell. L'Huilier's Theorem is used to compute the area of the triangles. This seems to be sufficiently accurate for elements on the Earth surface with edge lengths of approx. 100 m and gives results comparable to our implementation of Huilier's algorithm for edge lengths of up to 1 km.
Definition at line 396 of file area.c.
◆ yac_huiliers_area_info()
| double yac_huiliers_area_info | ( | struct yac_grid_cell | cell, |
| double * | barycenter, | ||
| double | sign | ||
| ) |
◆ yac_planar_3dcell_area()
| double yac_planar_3dcell_area | ( | struct yac_grid_cell | cell | ) |
Area calculation on a unit sphere of a planar polygon in 3D.
(http://gaim.umbc.edu/2010/06/03/polygon-area)
This area calculation works for any planar polygon (concave or convex) with non-intersecting edges in 3D. It requires vertex coordinates in Carthesian space. In our case this is applicable for very small elements on the sphere.
◆ yac_pole_area()
| double yac_pole_area | ( | struct yac_grid_cell | cell | ) |
Calculate the area of a cell in a 3d plane on a unit sphere.
see http://geomalgorithms.com/a01-_area.html
other references:
http://www.mathopenref.com/coordpolygonarea2.html
http://geomalgorithms.com/a01-_area.html
http://stackoverflow.com/questions/2350604/get-the-area-of-a-3d-surface
- Parameters
-
[in] cell cell for which the area shall be calculated
- Returns
- area of the cell
Definition at line 279 of file area.c.

◆ yac_triangle_area()
| double yac_triangle_area | ( | struct yac_grid_cell | cell | ) |
Calculate the area of a triangle on a unit sphere.
Adopted from the ICON code, mo_base_geometry.f90 provided by Luis Kornblueh, MPI-M.
The algorithm is based on Girards' theorem and formula.
Converted to c by Rene Redler, MPI-M.
Vertex coordinates need to be provided as cartesian coordinates
The algorithm is based on Girards' theorem and formula.
R: Earth radius n: number of vertices pi: guess what Theta: Sum of inner angle of the element (in rad)
The Formula reads as
S = [ Theta - (n-2) * pi ] * R*R
Ad with n=3 for triangles simplifies to
S = [ Theta - pi ] * R*R
- Parameters
-
[in] cell cell for which he area shal be calculated
- Returns
- approximate area of the cell
Definition at line 21 of file area.c.