Introduction
During the run of a coupled setup it can happen that field masks are changing (for example due to rising or falling sea levels). Unfortunatly, weights are only computed in the initialisation phase of the coupler. In addition, this is a time consuming process. Hence, reinitialisation of the coupler after each change of a mask is not a viable option, most of the time.
Instead of recomputation of all weights, it is also possible to provide an additional mask to the put operation. This mask can be used at each exchange step to adjust the weights, which were computed in the initialisation phase.
Description
When using dynamic fractional masking, the user has to provide masking values for all source points in an exchange. The masking values have to be in the range from 0.0 to 1.0.
In an exchange all source field values are multiplied by the fractional mask values. These values are then used to compute preliminary target field values. Afterwards each target field value is divided by the sum of the weights, used to compute the respected value, multiplied by the associated fractional mask value.
If 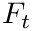
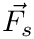
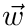
![\[
F_t=\vec{F_s}\cdot\vec{w}
\]](../../form_3.png)
If 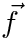
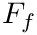
![\[
\begin{split}
f' & = \vec{f}\cdot\vec{w} \\
F'_t & = (\vec{F_s}\odot\vec{f})\cdot\vec{w} \\
F_t & = \begin{cases}
F'_t / f' & f' \not = 0 \\
F_f & f' = 0
\end{cases}
\end{split}
\]](../../form_6.png)
Example
In the following example a target point (blue dot) is interpolated by the average ( 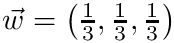
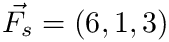
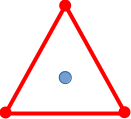
| Without fractional mask | With fractional mask: | With fractional mask: |
|---|---|---|
|
|
|
Usage in YAC
In order to use dynamic fractional masking, the user has to explicitly enable it (see Enabling dynamic fractional masking). This is only possible for field that have already been defined (see Definition of Coupling Fields).
If a field was enabled for dynamic fractional masking, the user has to provide a mask for all field values in all exchanges, where this field is used as a source (see yac_cput_frac, yac_cput_frac_, yac_cput_frac_ptr_, yac_cexchange_frac, yac_cexchange_frac_, yac_cexchange_frac_ptr_, yac_fput_frac_*, and yac_fexchange_frac_*).
Remark
The usage of dynamic fractional masking only makes sense for interpolation, where the weights for each target field value sum up to 1.
Acknowledgement
The implementation of dynamic fractional masking in YAC is based on the work of the same feature in OASIS3-MCT 6.0.
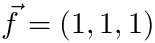
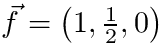
![\[
\begin{split}
F_t & = \left ( 6, 1, 3 \right )\cdot
\left ( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \right ) \\
& = 3.\bar{3} \\
\end{split}
\]](../../form_11.png)
![\[
\begin{split}
f' & = \left ( 1, 1, 1 \right )\cdot
\left ( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \right ) = 1 \\
F'_t & = \left (\left ( 6, 1, 3 \right )\odot
\left ( 1, 1, 1 \right ) \right )\cdot
\left ( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \right ) \\
& = \left ( 6, 1, 3 \right )\cdot
\left ( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \right ) \\
& = \frac{10}{3} \\
F_t & = \frac{10}{3} / 1 \\
& = 3.\bar{3} \\
\end{split}
\]](../../form_12.png)
![\[
\begin{split}
f' & = \left ( 1, \frac{1}{2}, 0 \right )\cdot
\left ( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \right ) =
\frac{1}{2} \\
F'_t & = \left (\left ( 6, 1, 3 \right )\odot
\left ( 1, \frac{1}{2}, 0 \right ) \right )\cdot
\left ( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \right ) \\
& = \left ( 6, \frac{1}{2}, 0 \right )\cdot
\left ( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \right ) \\
& = \frac{13}{6} \\
F_t & = \frac{13}{6}/\frac{1}{2} \\
& = 4.\bar{3}
\end{split}
\]](../../form_13.png)